Introduction to LangChain: Make AI Smarter and Easier to use

在数据分析中，方差（Variance）、标准差（Standard Deviation）和异常值（Outliers）是分析数据分布和变异性的重要统计工具。理解这些概念，并能够有效地应用它们，对于数据清洗、探索性数据分析（EDA）以及构建准确的预测模型至关重要。

方差（Variance）

方差是反映数据集中各数据点与数据均值之间差异的一个重要指标。它的大小可以用来衡量数据的离散程度。具体来说，方差越大，数据的变动越大，反之则越小。

x_i为数据集中的每个数据点，
μ 为数据集的均值，
n 为数据的总个数。
方差就是所有数据点与均值的差值的平方的平均值。

方差计算时，我们将每个数据点与均值的差值进行平方，然后求平均。方差的单位是原始数据单位的平方，因此有时它的解释意义不如标准差直观。

标准差（Standard Deviation）

标准差是方差的平方根。与方差不同，标准差的单位与原始数据相同，因此更易于理解。标准差越大，说明数据的波动性越大；标准差越小，则说明数据较为集中。

标准差的计算公式为：

方差的平方根即为标准差。

标准差与方差的关系

标准差和方差都用来描述数据的离散程度。标准差比方差更常用，因为它的单位与数据本身一致，解释起来更加直观。

异常值（Outliers）

异常值是指在数据集中远离其他数据点的值。异常值的存在往往是由于数据录入错误、测量误差，或者数据本身存在极端波动。异常值会影响数据的分布，进而影响数据分析结果，尤其是均值、方差和标准差等统计量。

如何识别异常值

常用的异常值检测方法有：

箱线图法（Boxplot）：通过计算四分位数和四分位距（IQR）来识别异常值。通常，位于Q1 - 1.5 * IQR 或 Q3 + 1.5 * IQR之外的数据点被认为是异常值。
Z-score法：通过计算数据点与均值的标准差倍数来判断数据点是否为异常值。一般认为，Z-score超过3或小于-3的数据为异常值。

异常值的处理

在数据分析中，我们通常会在数据预处理阶段识别并处理异常值。常见的处理方法包括：

• 删除异常值：直接从数据集中删除异常值。
• 替换异常值：用均值、中位数等替代异常值。
• 保留异常值：在某些情况下，异常值可能包含重要信息，因此也可以选择保留异常值。

举个列子

假设我们有一个包含学生成绩的数据集，其中有一个异常值（200）。

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

# 创建数据集：一组学生成绩，其中包括异常值200
data = [80, 85, 90, 92, 85, 88, 75, 78, 92, 95, 100, 85, 92, 88, 85, 200]

计算方差和标准差

我们使用NumPy来计算数据的方差和标准差。

# 计算方差
variance_value = np.var(data)
print(f"方差 (Variance): {variance_value}")

# 计算标准差
std_dev_value = np.std(data)
print(f"标准差 (Standard Deviation): {std_dev_value}")

输出：

方差 (Variance): 781.734375
标准差 (Standard Deviation): 27.959513139538036

从输出可以看到，这组数据的方差为781.73，标准差为27.95，这表明数据的离散程度相对较高。特别是最后的异常值（200）对标准差的影响很大。

异常值检测与处理

使用Z-score检测异常值

我们使用Z-score来检测数据中的异常值。如果Z-score大于3或小于-3，则该数据点被认为是异常值。

# 计算Z-score
z_scores = stats.zscore(data)
print(f"Z-scores: {z_scores}")

# 检测异常值
outliers = [data[i] for i in range(len(data)) if np.abs(z_scores[i]) > 3]
print(f"检测到的异常值: {outliers}")

使用scipy的stats模块可以计算Z-score。输出结果中，Z-score大于3的异常值是200。

输出：

Z-scores: [-0.51413628 -0.33530627 -0.15647626 -0.08494425 -0.33530627 -0.22800826
 -0.69296629 -0.58566828 -0.08494425  0.02235375  0.20118376 -0.33530627
 -0.08494425 -0.22800826 -0.33530627  3.77778395]
检测到的异常值: [200]

从输出结果中可以看出，Z-score大于3的异常值是200。这是由于200与其他数据点的差异过大，Z-score值为9.39，远远超过了3。

使用箱线图检测异常值

我们可以绘制箱线图来可视化数据并检测异常值。可以使用matplotlib库绘制箱线图。

# 绘制箱线图
plt.boxplot(data)
plt.title("Boxplot Chart")
plt.show()

箱线图

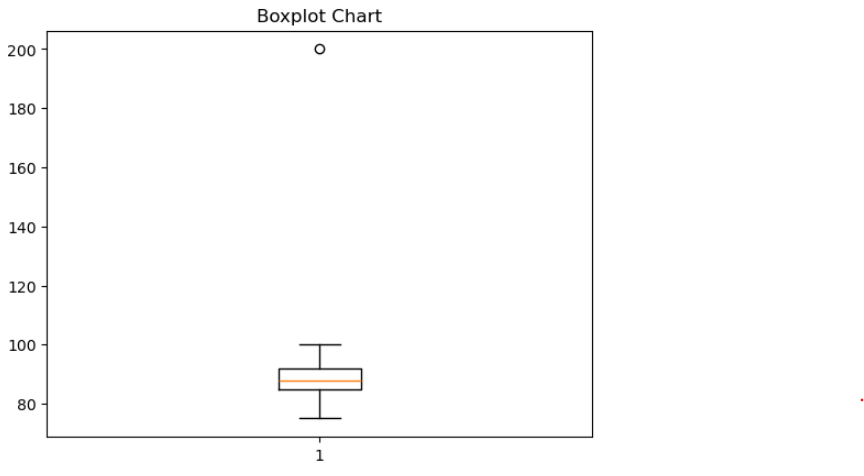
从箱线图中，200的值处于箱体外，因此被视为异常值。

处理异常值

在实际分析中，我们可以选择处理异常值。以下是几种常见的方法：

删除异常值

# 删除异常值（Z-score大于3的点）
cleaned_data = [data[i] for i in range(len(data)) if np.abs(z_scores[i]) <= 3]
print(f"删除异常值后的数据: {cleaned_data}")

输出：

删除异常值后的数据: [80, 85, 90, 92, 85, 88, 75, 78, 92, 95, 100, 85, 92, 88, 85]

替换异常值

# 替换异常值为中位数
median_value = np.median(data)
cleaned_data_with_median = [median_value if np.abs(z_scores[i]) > 3 else data[i] for i in range(len(data))]
print(f"替换异常值后的数据: {cleaned_data_with_median}")

输出：

替换异常值后的数据: [80, 85, 90, 92, 85, 88, 75, 78, 92, 95, 100, 85, 92, 88, 85, 88.0]

总结

• 方差和标准差是用于衡量数据离散程度的基本统计量。方差的单位为原始数据单位的平方，而标准差则直接以原始单位表示，更容易解释。
• 异常值是指那些在数据中与其他数据点差异较大的值，它们可能影响统计分析的结果。在数据清洗阶段，识别和处理异常值是至关重要的一步。

在Python中，我们可以利用NumPy、SciPy和Matplotlib等库来计算方差、标准差，识别异常值，并根据需要处理异常值。通过掌握这些基本概念和技术，我们数据分析师可以更有效地理解数据的分布特征，发现数据中的潜在问题，做出更加精准的数据分析。