Introduction to LangChain: Make AI Smarter and Easier to use

在数据分析中，理解数据的分布特征至关重要。四分位法（Quartile Method）是分析数据分布的一种基础方法，它通过将数据集划分为四个相等的部分，帮助我们揭示数据的集中趋势和离散程度。四分位法特别适合处理异常值和非对称分布的数据集。

本文将深入介绍四分位法的核心概念：第一四分位数 (Q1)、第二四分位数 (Q2)、第三四分位数 (Q3)、四分位距 (IQR)，并通过 Python 代码示例说明如何计算这些统计量，同时展示如何通过箱型图可视化这些数据特征。

四分位数 (Quartile)

四分位数是将排序后的数据集划分为四个相等的部。具体如下:

第一四分位数 (First Quartile, Q1)：数据集中的第 25% 位置，表示数据中有 25% 的数据小于 Q1。它是数据的第 25 百分位数。

第二四分位数 (Second Quartile, Q2)：数据集的中位数，表示 50% 的数据小于 Q2，50% 的数据大于 Q2，也叫数据的第 50 百分位数。

第三四分位数 (Third Quartile, Q3)：数据集中的第 75% 位置，表示数据中有 75% 的数据小于 Q3。

四分位距 (Interquartile Range, IQR)，它是 Q3 和 Q1 之间的差值，用来衡量数据的分散程度：

IQR = Q3 - Q1

四分位距对于识别异常值非常有帮助，它可以帮助我们判断哪些数据点可能是极端值。

比如，我们有如下学生成绩分数的数据

80, 85, 90, 92, 85, 88, 75, 78, 92, 95, 100, 85, 92, 88, 85, 200

使用Python计算四分位数和四分位距， Python 中的numpy库提供了 percentile 函数来计算四分位数。代码如下：

import numpy as np

data = [80, 85, 90, 92, 85, 88, 75, 78, 92, 95, 100, 85, 92, 88, 85, 200]

# 计算第一四分位数
Q1 = np.percentile(data, 25)
print(f"Q1 = {Q1}")

# 计算第二四分位数,第二四分位数就是中位数,也可以使用 `np.median(data)`
Q2 = np.percentile(data, 50)
print(f"Q2 = {Q2}")

# 计算第三四分位数
Q3 = np.percentile(data, 75)
print(f"Q3 = {Q3}")

# 计算四分位距
IQR = Q3 - Q1
print(f"IQR = {IQR}")

输出结果如下：

Q1 = 85.0
Q2 = 88.0
Q3 = 92.0
IQR = 7.0

四分位数的应用

数据分布分析

四分位数能够帮助我们快速了解数据的分布情况。对于一些非正态分布的复杂数据集，四分位数比均值和标准差更能准确地反映数据的真实情况。

识别异常值

通过计算 IQR，我们可以根据以下规则识别异常值：

如果数据小于 Q1 − 1.5 x IQR，则视为低于正常范围的异常值。
如果数据大于 Q3 + 1.5 × IQR，则视为高于正常范围的异常值。

下面使用这个方式来找出上面学生成绩中的异常值, Python代码如下:

# 计算异常值
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR

# 找出异常值
outliers = [x for x in data if x < lower_bound or x > upper_bound]

print(f"异常值 (Outliers): {outliers}")

输出结果如下：

异常值 (Outliers): [200]

数据可视化

箱型图（Boxplot）是一种通过展示四分位数和数据分布的图形化工具。它能够帮助我们快速识别数据的集中趋势、分散程度以及潜在的异常值。

箱型图 (BoxPlot)

箱型图是一种常用的图表，它能够直观地呈现数据分布的形态，是基于四分位法的一种有效可视化方式。可视化四分位法需要使用Python的 matplotlib 库。代码如下：

import matplotlib.pyplot as plt

# 绘制箱型图
plt.boxplot(data)
plt.title('Student Score Boxplot')
plt.xlabel('data')
plt.ylabel('Score')
plt.show()

使用plt.boxplot()函数绘制箱型图，它会自动计算并显示数据的四分位数、异常值以及数据的分布情况。

输出结果如下：

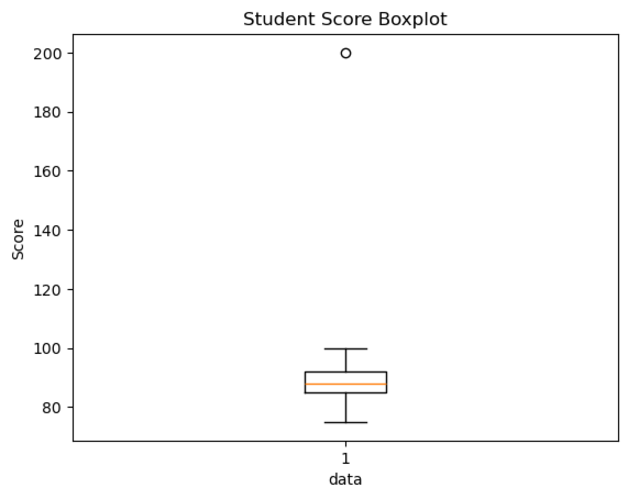
上面的箱型图的内容包括如下：

箱体：表示从 Q1 到 Q3 的范围，即数据中 50% 的值。
中位线：箱体内的线表示 Q2（中位数），即数据的中间值。
须：箱体外部的线表示数据的最小值和最大值，排除了异常值。
异常值：任何超出 Q1−1.5×IQR 或 Q3+1.5×IQR 范围的数据点将显示为单独的点。

所以从上面的箱型图中，我们可以看出，学生的成绩分布非常集中，数据集中位数为 88，四分位数分别为 85 和 92，IQR 为 7。并且异常值是200分，它位于 Q3+1.5×IQR 之外，因此可以视为异常值。

总结

概括下来就是：

1. 四分位法是分析数据分布的一种基础方法，它通过将数据集划分为四个相等的部分，帮助我们揭示数据的集中趋势和离散程度。
2. 四分位数是将排序后的数据集划分为四个相等的部。
3. 四分位数能够帮助我们快速了解数据的分布情况。对于一些非正态分布的复杂数据集，四分位数比均值和标准差更能准确地反映数据的真实情况。
4. 箱型图是一种常用的图表，它能够直观地呈现数据分布的形态，是基于四分位法的一种有效可视化方式。
5. 箱型图能够帮助我们快速识别数据的集中趋势、分散程度以及潜在的异常值。